個別指導塾・学習塾のナビ個別指導学院

周南市周辺にお住まいの皆さん
いつも当ブログをご覧くださりありがとうございます！
ナビ個別指導学院徳山校です。

山口県の入試問題で必ず出るといっても過言ではない「関数」。
中1の比例、反比例から中2の1次関数、中3のｙ＝αｘ²の関数とつながっています。
　
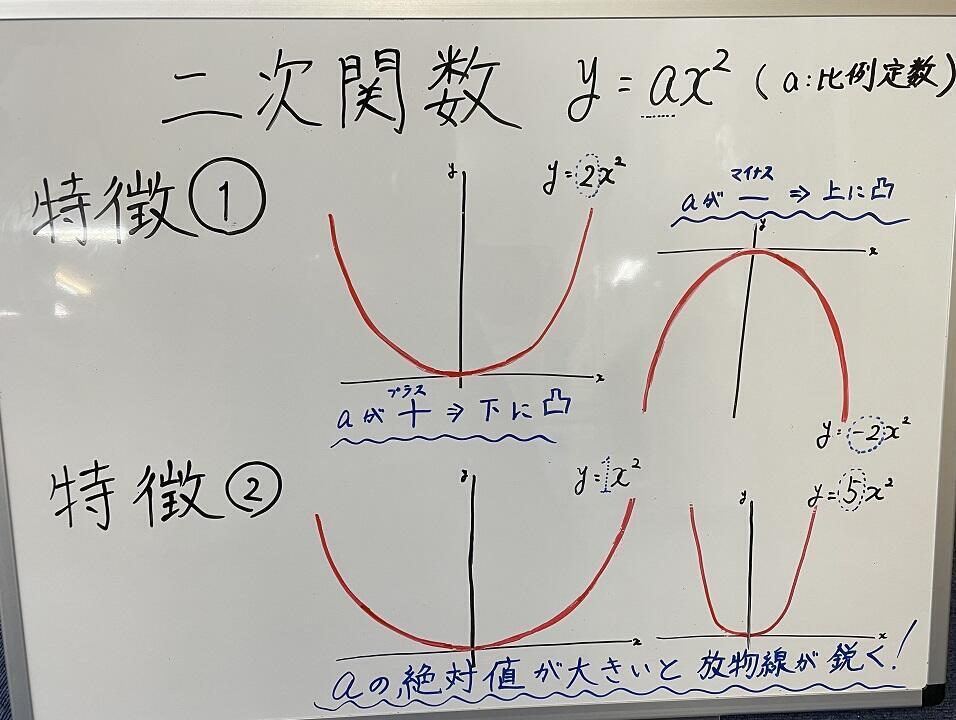
特に苦手な生徒が多いのがｙ＝αｘ²の関数です。
グラフを書く、グラフから式を読み取る、変化の割合を求める、変域を求める、動点　etc
と出題内容も多岐にわたります。
　
たくさん問題を解いて慣れることも必要ですが、まずは解き方を正確に理解することが大切です。
今回は2次関数の変化の割合を簡単に求める方法をお伝えします！

　
問題：関数ｙ＝3ｘ²についてⅹの値が２から５まで増加するときの変化の割合を求めなさい
　
基本の解き方は、xの増加量とｙの増加量を考えて計算しますね！
xの増加量が2→5なので3
ｙの増加量は y=3x²のｘに2を代入して12、
y=3x²に5を代入して75 12→75なので
ｙの増加量は63 計算すると変化の割合は21となります。
ここで簡単に求められる公式a(p＋q)を使うと一瞬で答えにたどり着きます！
　
a(p＋q)　この公式に先程の問題の数字を代入すると
3(2＋5)＝21 と簡単に答えを求めることができます！
これ以外にも簡単に求められる公式や覚え方のコツをナビ個別では指導していきます！
　
無料体験授業も好評受付中！
ぜひ一度お越しください！いつでもお待ちしております～

ナビ個別指導学院徳山校

０１２０－９４１－９６７

教室営業時間：火～土　１５：００～２１：３０

フリーダイヤル受付：火～土　１２：００～２１：００

高校入試で必須の「二次関数」